1. 函数
1.1. 函数定义
函数是将一个对象转化为另一个对象的规则. 起始对象称为输入, 即定义域. 返回对象称为输出, 所有可能输出的集合为上域, 所有实际输出的集合为值域. 如 f(x)=x^2, 上域为R, 值域为非负数.
形如 \$f(x)=mx+a\$的函数称为线性函数.
1.2. 区间表示法
[a,b]表示从a端点到b端点的所有实数, 包括a和b, 称为闭区间. (a,b)表示从a端点到b端点的所有实数, 但不包括a和b, 称为开区间.
1.3. 反函数
给定一个函数f,在f的值域中选择y.仅有一个y值满足f(y)=x.
-
只有唯一的x值能满足f(x)=y
-
f-1 的定义域和f的值域相同
-
f-1的值和f的定义域相同
-
\$f^-1(y)\$ 满足 y=f(x)
-
\$(f@(f^-1))(x)=x\$
-
反函数的反函数在一定定义域内就是原函数
-
水平线校验: 如果每条水平线和函数图像相交最多一次, 则这个函数就有一个反函数.
-
几何定义: 原函数和反函数关于y=x对称.
-
将等式变换为x=f(y)
-
交换x/y的位置, 使得y=f(x)
1.4. 函数的复合
\$f(x)=h(g(x))\$, f是g与h的复合. 记为 \$f=h@g\$
1.5. 奇偶函数
-
奇函数: \$f(x) = -f(-x)\$
-
偶函数: \$f(x) = f(-x)\$
f(x)=0 既是奇函数又是偶函数
1.6. 指数函数
1.6.1. 指数函数性质
-
\$a^x*a^y=a^(x+y)\$
-
\$a^x/a^y=a^(x-y)\$
-
\$(a^x)^y=a^(x*y)\$
-
\$a^x*b^x=(a*b)^x\$
-
\$a^x/b^x=(a/b)^x\$
1.6.2. 指数增长/衰减
\$y=P*e^(kx)\$ (k>0时指数增长, k<0时指数衰减)
1.7. 对数函数
1.7.1. 对数函数性质
-
\$a^(log_ax)=x\$
-
\$log_a(x*y)=log_ax+log_ay\$
-
\$log_a(x/y)=log_ax-log_ay\$
-
\$log_ax^y=ylog_ax\$
-
\$a^x=e^(lna^x)=e^(x*lna)\$ 如: \$2^x=e^(ln2x)\$
-
\$lnx=lna^(log_ax)=log_ax*lna => log_ax=lnx/lna\$
换底公式
1.8. 三角函数
1.8.1. 定义
-
\$正弦sin(theta)=(对边)/(斜边),余割csc(x)=1/sin(x) ['kəu'si:kənt\$]
-
\$余弦cos(theta)=(邻边)/(斜边),正割sec(x)=1/cos(x) ['si:kənt\$]
-
\$正切tan(theta)=(对边)/(邻边),余切cot(x)=1/tan(x)\$
对称性: sin/csc/tan/cot为奇函数, cos/sec为偶函数
1.8.2. 常见三角函数值
| 0 | \$pi/6\$ | \$pi/4\$ | \$pi/3\$ | \$pi/2\$ | |
|---|---|---|---|---|---|
sin |
0 |
\$1/2\$ |
\$1/sqrt(2)\$ |
\$sqrt(3)/2\$ |
1 |
cos |
1 |
\$sqrt(3)/2\$ |
\$1/sqrt(2)\$ |
\$1/2\$ |
0 |
tan |
0 |
\$1/sqrt(3)\$ |
1 |
\$sqrt(3)\$ |
- |
1.8.3. 周期函数
对于函数f, 如果存在某个正整数p使得\$f(x+p)=f(x)\$, 最小的这样的p值称为函数f的周期.
-
tan,cot周期为\$pi\$
-
sin,cos,csc,sec周期为\$2pi\$
1.8.4. 毕达哥拉斯定理
\$cos^2(x)+sin^2(x)=1\$
等式两边除以cos2(x)得: \$1+tan^2(x)=sec^2(x)\$
等式两边除以sin2(x)得: \$1+cot^2(x)=csc^2(x)\$
1.8.5. co(互余)
-
\$sin(x)=cos(pi/2-x)\$
-
\$tan(x)=cot(pi/2-x)\$
-
\$sec(x)=csc(pi/2-x)\$
反之也成立
1.8.6. 倍角公式
-
\$sin(A+B)=sin(A)cos(B)+cos(A)sin(B)\$
-
\$cos(A+B)=cos(A)cos(B)-sin(A)sin(B)\$
-
\$sin(2x)=2sin(x)cos(x)\$
-
\$cos(2x)=2cos^2(x)-1=1-2sin^2(x)\$
1.8.7. 余弦定理
\$c^2=a^2+b^2-2abcostheta\$
推导: \$c^2=(asintheta)^2+(b-scostheta)^2=a^2*(sin^2theta+cos^2sintheta)-2abcostheta+b^2=a^2+b^2-2abcostheta\$
1.8.8. 三角函数的反函数
-
\$cos^-1(-x)+cos^(-1)x=pi\$
-
\$sin^-1x+cos^-1x=pi/2\$
1.8.9. 椭圆方程
\$x^2/a^2+y^2/b^2=1\$
1.10. 判别式
\$Delta=(-b+-sqrt(b^2-4ac))/(2a)\$
Delta大于0时有两个不同的解. 等于0时有一个解. 小于0时在实数范围内无解.
\$c^2=a^2+b^2-2ab*cos(theta)\$
1.11. 立方差公式
\$a^3-b^3=(a-b)(a^2+ab+b^2)\$
1.13. 回归方程
-
\$y=mx+b\$
-
\$y=ax^2+bx+c\$
-
\$y=a*x^b\$
-
\$y=a*e^bx\$
-
\$y=alnx\$
-
\$y=asin(bx+p)+c\$
2. 极限和连续
2.1. 极限定义
-
非正式定义: 当x趋于a时,f趋于极限L, 记作 \$lim_(x->a)f(x)=L\$
-
正式定义: 如果对任何数 \$epsilon>0\$,存在相应的数 \$delta>0\$使得对所有满足 \$0<|x-x_0|<delta\$的 \$x\$,有 \$|f(x)-L|<epsilon\$
2.2. 极限不存在的情况
-
跳跃间断: 左极限不等于右极限.. 如 \$f(x)={(1,x<=0),(0,x>0):}\$
-
无穷间断: 极限无穷大或无穷小. 如 \$f(x)=1/x\$.
-
震荡间断: 函数不停振荡,没有极限. 如 \$f(x)=sin(1/x)\$.
| 当且仅当左右极限存在并相等时极限才存在. |
2.3. 极限法则
-
\$lim_(x->c)(f(x) + g(x))=L+M\$
-
\$lim_(x->c)(f(x) - g(x))=L-M\$
-
\$lim_(x->c)(f(x) * g(x))=L*M\$
-
\$lim_(x->c)f(x) / g(x)=L/M\$
-
\$lim_(x->c)(k*f(x))=k*L\$
-
\$lim_(x-c)f(x)^(r/s)=L^(r/s)\$
2.4. 求极限
2.4.1. 多项式
多项式直接代入算出极限.
2.4.2. \$lim_(x->a)(p(x))/(q(x))\$
-
将a代入函数, 如果分母不为0, 则代入后计算出的值即为极限值.
-
因式分解, 尝试消除分母.
-
乘以共轭不等式,消除公因子.
-
如果分母为0, 分子不为0时, 在x=a时会有一条垂直渐近线, 根据a左右的符号来计算函数的极限 (\$-oo | oo | DNE\$).
2.4.3. \$lim_(x->oo)(p(x))/(q(x))\$
-
如果p的次数等于q的次数, 则该多项式有极限且非零.
-
如果p的次数大于q的次数, 则极限是 \$oo\$ 或 \$-oo\$
-
如果p的次数小于q的次数, 则极限是0.
2.5. 三明治定理
对于所有在 \$a\$ 附近的 \$x\$ 都有 \$g(x)<=f(x)<=h(x)\$,且 \$lim_(x->a)g(x)=lim_(x->a)h(x)=L\$, 则 \$lim_(x->a)f(x)=L\$.
2.5.1. 求极限 \$lim_(x->oo)sin(x)/x\$:
-
\$-1<=sin(x)<=1\$
-
\$-1/x<=sin(x)/x<=1/x\$
-
\$:' lim_(x->oo)(-1/x)=lim_(x->oo)1/x=0\$
-
\$:. lim_(x->oo)sin(x)/x=0\$
2.5.2. 求极限 \$lim_(x->0)sin(x)/x\$
-
\$sin(x)<x<tan(x)\$
-
除以sin(x)得: \$1<x/sin(x)<1/cos(x)\$
-
取倒数得: \$cos(x)<sin(x)/x<1\$
-
\$:' lim_(x->0)cos(x)=1\$
-
\$:. lim_(x->0)sin(x)/x=1\$
2.6. 洛必达法则
\$lim_(x->a)f(x)/g(x)=lim_(x->a)(f'(x))/(g'(x))\$
-
\$0/0\$
-
\$oo/oo\$
-
\$oo - oo\$
通分或同时乘以/除以一个共轭表达式 -
\$0 * oo\$
选一个因式取倒数移到分母 -
\$1^(+-oo) | 0^0 | (oo)^0 \$
先求对数再求指数的极限
2.7. 三角函数的极限
-
\$lim_(x->0)sin(x)/x = 1\$
-
\$lim_(x->0)cos(x) = 1\$
-
\$lim_(x->0)tan(x)/x = 1\$
-
\$lim_(x->0)cos(x)/x = DNE\$
-
\$lim_(x->oo)sin(**)/x^alpha=0\$
2.8. 渐近线
2.8.1. 水平渐近线
如果\$lim_(x->oo)f(x)=lim_(x->-oo)f(x)=b\$, 则y=b是水平渐近线.
2.8.2. 垂直渐近线
令分母为0求出x=a, 如果\$lim_(x->a)f(x)=+-oo\$, 则x=a为垂直渐近线.
2.9. 连续的定义
如果\$lim_(x->x_0)f(x) = f(x_0)\$, 则函数在点 \$x=x_0\$ 上连续.
-
点 \$x_0\$ 在函数的定义域内.
-
\$lim_(x->x_0)f(x)\$ 在点 \$x=x_0\$ 的左极限等于右极限.
-
函数值和函数在该点的极限值相等.
使用两个连续函数做加减乘除, 所得出的新的函数也是连续函数.
2.10. 区间连续
如果函数f在(a,b)上每一点都连续, \$lim_(x->a^+)f(a)=f(a) 且 lim_(x->b^-)f(b)=f(b)\$, 则f在 [a,b]这个区间上连续.
2.11. 介值定理
如果函数f在区间[a,b]上连续, 且f(a)<0, f(b)>0, 则(a,b)间至少有一点c, 满足f(c)=0.
2.12. 最大值最小值
如果函数f在区间[a,b]上连续, 则f在[a,b]上至少有一个最小值和最大值.
3. 导数
3.1. 定义
函数 \$f(x)\$ 在 \$x_0\$ 的导数, 即为过该点的切线的斜率, 记为 \$f'(x)=lim_(Deltax->0)(Deltay)/(Deltax)=(dy)/(dx)\$
| 函数在一点有导数(可微)当且仅当该函数有左侧导数和右侧导数且相等. |
3.2. 表示
-
牛顿表示法: \$f^'(x)\$
-
莱布尼兹表示法: \$dy/dx\$ \$(df)/(fx)\$ \$d/dxf\$ \$d/dxy\$
3.3. 求导法则
-
\$d/dx(c)=0\$
-
\$d/dxx^n=n*x^(n-1)\$
-
\$d/dx(cu)=c*(du)/dx\$
-
\$d/dx(u+v)=(du)/dx+(dv)/dx\$
-
\$(cu)'=c(u)'\$
-
\$(u*v)'=u(v)'+(u)'v\$
-
\$(u/v)'=(u'v-v'u)/v^2\$
-
\$dy/dt=dy/dx*dx/dt\$
链式法则 -
\$D^nx^n=n!\$
3.4. 三角函数的导数
-
\$(sin(x))'=cos(x)\$
-
\$(cos(x))'=-sin(x)\$
-
\$(tan(x))'=sec^2(x)\$
-
\$(csc(x))'=-csc(x)cot(x)\$
-
\$(sec(x))'=sec(x)tan(x)\$
-
\$(cot(x))'=-csc^2(x)\$
3.5. 隐函数求导
-
等式两边同时求导.
-
将 \$dy/dx\$ 提取到等式一边, 解出 \$dy/dx\$.
3.6. 可导必连续
如果一个函数f在x上可导, 那么它在x上连续. 但连续不一定可导, 如 f(x)=|x|.
需要证明的等式: \$lim_(h->0)f(c+h)=f(c)\$
-
\$f(c+h)=f(c) + (f(c+h)-f(c))=f(c)+ (f(c+h)-f(c))/ h * h\$
-
\$lim_(h->0)f(c+h)=lim_(h->0)f(c)+lim_(h->0)(f(c+h)-f(c))*lim_(h->0)h\$
-
\$lim_(h->0)f(c+h)=lim_(h->0)f(c)=f(c)\$. 得证
3.7. 导数的应用
3.7.1. 求极值
连续函数的最大值M,最小值m使得 \$m<=f(x)<=M\$
-
计算函数端点和临界点(\$f'(x)=0\$)的值.
-
比较大小, 得出最大值和最小值.
证明: 临界点的左右两侧导数一边大于等于0, 一边小于等于0, 所以临界点的导数等于0.
3.7.2. 罗尔定理
可微曲线在与x轴相交的两点之间必有一点导数为0.
3.7.3. 中值定理
函数在(a,b)区间内可微, 在[a,b]上连续, 则中间必有一点c满足 \$f'(c)=(f(b)-f(a))/(b-a)\$
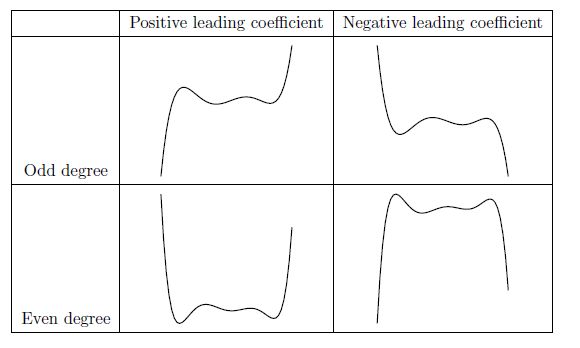
3.8. 绘制函数图像
-
检查函数奇偶性.
-
计算y轴截距.
-
计算x轴截距.
-
求出函数的定义域.
-
找到函数的垂直渐近线 (分母为0).
-
根据函数的零点计算函数的正负.
-
找到函数的水平渐近线(\$lim_(x->oo)f(x)\$).
-
根据一阶导数判断函数的上升下降趋势.
-
解出f'(x)=0, 找到最值.
-
根据二阶导数判断函数的凹凸性.
3.8.1. 线性近似
\$f(x)~~f(x_0) + f'(x_0)(x-x_0) + (f''(x_0))/2(x-x_0)^2\$
-
\$(1+x)^k~~kx+1\$
-
\$sinx~~x\$
-
\$cosx~~1\$
-
\$tanx~~x\$
3.8.2. 牛顿迭代法
\$x_1=x_0-f(x_0)/(f'(x_0))\$
3.9. 自然对数
\$e=lim_(n->oo)(1+1/n)^n=lim_(h->0)(1+h)^(1/h)\$
-
\$n->oo,令 Deltax = 1/n -> 0\$
-
\$ln((1+1/n)^n) = nln(1+1/n)\$
-
\$lim_(n->oo)nln(1+1/n)=1/Deltaxln(1+Deltax) = d/(dx)lnx|_(x=1) = 1/x|_(x=1) = 1\$
-
\$lim_(n->oo)ln((1+1/n)^n)=1\$
-
\$e^(lim_(n->oo)ln((1+1/n)^n))=lim_(n->oo)(1+1/n)^n=e\$
3.10. 对数求导
-
\$(log_bx)'=1/xlog_be\$
-
\$(lnx)'=1/x\$
-
\$(b^x)'=b^xlnb\$
-
\$(e^(ax))'=ae^(ax)\$
-
\$(x^(a))'=ax^(a-1)\$
3.11. 对数的极限
-
\$lim_(h->0)(e^h-1)/h=1\$
-
\$lim_(h->0)ln(1+h)/h=1\$
-
\$lim_(x->oo)x^n/e^x=0\$
-
\$lim_(x->oo)e^x=oo\$
-
\$lim_(x->oo)lnx/x^a=0\$
4. 积分
4.1. 不定积分
通过导数求原函数
\$G(x)=intg(x)dx,(G'(x)=g(x))\$
-
\$intx^adx=x^(a+1)/(a+1)+C,(a!=-1)\$
-
\$intsinkxdx=-(coskx)/k+C\$
-
\$intcoskxdx=(sinkx)/k+C\$
-
\$intsec^2xdx=tanx+C\$
-
\$intcsc^2xdx=-cotx+C\$
-
\$intsecxtanxdx=secx+C\$
-
\$intcscxcotxdx=-cscx+C\$
-
\$intdx/x=ln|x|+C,(x!=0)\$
-
\$intsin^2xdx=int(1-cos2x)/2dx=1/2int(1-cos2x)dx=x/2-(sin2x)/4+C\$
-
\$intcos^2xdx=int(1+cos2x)/2dx=x/2+(sin2x)/4+C\$
如果两个函数的导数相同: \$F'(x)=G'(x),则 F(x)=G(x)+C\$.
4.2. 不定积分法则
-
\$intkf(x)dx=kintf(x)dx\$
-
\$int-f(x)dx=-intf(x)dx\$
-
\$int(f(x) +- g(x))dx=intf(x)dx +- intg(x)dx\$
4.3. 求积分方法
-
换元法: \$t=f(x),dt=f'(x)dx\$
-
分部积分: \$int_a^buv'dx=uv|_(b-a) - int_a^bu'vdx\$
-
部分分式
-
三角替换
4.4. 求和
\$sum_(j=a)^b(f(j)-(f-1))=f(b)-f(a-1)\$
-
\$sum_(j=1)^n(j^2-(j-1)^2)=sum_(j=1)^n(2j-1)=n^2\$
-
\$sum_(j=1)^n(j^3-(j-1)^3)=sum_(j=1)^n(3j^2-3j+1)=n^3\$
4.5. 定积分
黎曼和: \$int_a^bf(x)dx=lim_(mesh->0)sum_(j=1)^nf(c_j)(x_j-x_(j-1))\$
-
\$int_a^bf(x)dx=-int_b^af(x)dx\$.
-
\$int_a^af(x)dx=0\$.
-
\$int_a^cf(x)dx=int_a^bf(x)dx+int_b^cf(x)dx,a<b<c\$.
-
\$int_a^bCf(x)dx=Cint_a^bf(x)dx\$.
-
\$int_a^b(f(x)+g(x))dx=int_a^bf(x)dx+int_a^bg(x)dx\$.
-
\$若 f(x)<=g(x),则 int_a^bf(x)dx <= int_a^bg(x)dx\$.
-
\$int_(u_1)^(u_2)f(u)du=int_(x_1)^(x_2)g(u(x))u'(x)dx,du=u'(x)dx,u_1=u(x_1),u_2=u(x_2)\$.
当且仅当 u'(x) 没有改变符号的时候才成立.
4.6. 定积分的中值定理
如果函数f在闭区间[a,b]上连续, 那么在开区间(a,b)内总有一点c满足 \$f(c)=1/(b-a)int_a^bf(x)dx\$.
4.7. 微积分基本定理
-
若函数f在闭区间[a,b]上连续, \$F(x)=int_a^xf(t)dt,x in [a,b\$], 则 F(x)在开区间(a,b)是可导函数, 且F'(x)=f(x), 记为 \$d/dxint_a^xf(t)dt=f(x)\$
-
若函数f在闭区间[a,b]上连续, \$F'(x)=f(x)\$, 则 \$int_a^bf(x)dx=F(x)|_(b-a)\$.
-
\$y=int_1^(x^2)costdt\$
-
\$令u=x^2,du=2xdx\$
-
\$dy/dx=(dy)/(du)*(du)/(dx)=int_1^ucost * 2x=cosudu=2xcos(x^2)\$
-
-
\$求 int_-1^3(x^3+1)dx\$
-
\$int(x^3+1)dx=x^4/4+x\$
-
\$int_-1^3(x^3+1)dx = x^4/4+x|_(3-(-1)) = 24\$
-
5. 反常积分
5.1. 定义
如果函数f在闭区间[a,b]是无界的(有垂直渐近线),或 a为 \$-oo\$,或b为 \$oo\$, 则积分 \$int_a^bf(x)dx\$为反常积分.
如果反常积分能满足 \$int_a^bf(x)dx=lim_(epsilon->0+)int_(a+epsilon)^bf(x)dx\$, 则该积分是收敛的, 否则是发散的. 非反常积分自然收敛于常数L.
5.2. 性质
-
\$int_a^(oo)f(x)dx=lim_(N->oo)int_a^Nf(x)dx\$
-
\$int_1^oo1/xdx=lim_(N->oo)(lnN-ln1)dx=oo\$
-
\$int_1^oo1/x^2dx=lim_(N->oo)(-1/x-(-1))dx=1\$
-
-
\$int_(-oo)^bf(x)dx=lim_(N->oo)int_-N^af(x)dx\$
5.3. 判断收敛发散
-
比较判别法: \$f(x)>=g(x)=oo\$
-
p判别法: 积分\$int_a^oo1/x^pdx (p>1)和 int_0^a1/x^pdx (p<1)\$是收敛的.
6. 数列和级数
6.1. 数列
一组有序的数称为数列, 无穷项的数列称为无穷数列. 当n趋近于\$oo\$时, 数列的极限记为 \$lim_(n->oo)a_n\$. 若存在极限值L, 则称该数列收敛于L, 否则该数列是发散的.
6.2. 级数
级数就是和, 就是将数列前n项相加. \$A_n=sum_(n=1)^Na_n\$, 无穷级数记为 \$sum_(n=1)^ooa_n=lim_(n->oo)sum_(n=1)^ooa_n\$.
6.4. 几何级数
\$1+r+r^2+r^3+...+r^n=sum_(n=0)^oor^n=(1-r^(n+1))/(1-r)\$
无穷几何级数: 若 \$-1<r<1,r_1+r_2+r_3+...=r_1/(1-r)\$, 否则级数发散.
6.5. 判断级数发散还是收敛
-
第n项判别法
若 \$lim_(n->oo)a^n !=0\$或极限不存在, 则级数 \$sum_(n=0)^ooa^n\$发散.
第n项判别法 不能作为级数收敛的判断.
|
-
比式判别法
若级数中包含阶乘或指数, 可以使用比式判别法: 令 \$L=lim_(n->oo)|a_(n+1)/a_n|\$, 若L>1,则该级数发散, 若L<1, 该级数收敛. 但当L=1或极限不存在时, 比式判别法无效.
-
根式判别法
令 \$L=lim_(n->oo)|a_n|^(1/n)\$, 若L<1时该级数收敛, L>1时该级数发散. 若L=1或极限不存在, 根式判别法无效.
-
积分判别法
当级数含有\$1/n和ln(n)\$时, 可以应用积分判别法: 对于连续递减函数 \$f(n)=a_n,则sum_(n=N)^ooa_n与 int_N^oof(x)dx\$ 同时收敛或同时发散.
-
p判别法
若 \$a>=1\$, 则级数 \$sum_(n=a)^oo1/n^p{(收敛,,p>1),(发散,,p<=1):}\$
6.6. 泰勒定理
\$f(x)=sum_(n=0)^Nf^(n)(a)/(n!)(x-a)^n+f^(N+1)(c)/((N+1)!)(x-a)^(N+1)\$
6.7. 幂级数
\$sum_(n=0)^oof^(n)(a)/(n!)(x-a)^n\$, 该级数称为 泰勒级数, a=0时称为 麦克劳林级数.
example: \$e^x=1+x+x^2/(2!) + x^3/(3!)+...\$